看点 杨振宁和当代数学

　　情况如下:杨振宁和陈省身的早期交往1922年，杨振宁出生于中国东部的一个中等城市——合肥。他的父亲杨克纯YangKo-Chuen，又名杨武之是北平清华大学教授，其后任复旦大学教授。杨武之于1928年在狄克逊L.E.Dickson指导下，以数论研究获芝加哥大学博士学位。他是把现代数学引入中国的先驱之一，教导过许多优秀的学生，其中有两位最著名:华罗庚和陈省身。

　　杨振宁和陈省身的早期交往

　　1922年，杨振宁出生于中国东部的一个中等城市——合肥。他的父亲杨克纯(YangKo - Chuen，又名杨武之) 是北平清华大学教授，其后任复旦大学教授。杨武之于1928年在狄克逊 (L. E. Dickson) 指导下，以数论研究获芝加哥大学博士学位。他是把现代数学引入中国的先驱之一，教导过许多优秀的学生，其中有两位最著名:华罗庚和陈省身。

　　张：您第一次见到陈省身教授是在什么时候?

　　杨：1930-1934年，陈教授在北平清华大学做研究生时，我父亲是清华数学系教授，但我不记得那时我们是否见过面。然而我却清楚记得首次见到陈夫人时的情景。那是在1929年10月初，她的父亲郑桐荪教授已在清华做了好几年教授，杨家则刚搬到清华。那时我只有7岁，在上小学。郑教授一家邀请我们到他家里吃饭。于是我第一次见到了“郑姊姊”。郑杨两家的关系一直十分密切。1939年，我父亲和母亲更撮合了陈教授与郑士宁女士的婚事，并且因此成为他们在昆明结婚时的介绍人。

　　张：1938-1942年间，您是清华大学物理系的学生，陈省身先生是否教过您?

　　杨：1937年陈教授学成回国。当时由于抗日战争，清华大学与北京大学、南开大学在昆明合并组成战时的国立西南联合大学，即西南联大。陈先生在西南联大教了六年书：1937—1943。他是一位极出色和受欢迎的教授。我则先在西南联大读本科，然后念研究生。西南联大的岁月在我脑海中留下了美好的回忆，当时所受的优良教育也令我终生感激。

　　在西南联大，我很可能旁听过陈省身的好几门数学课，但是根据保存至今的成绩单，我只是在1940年秋季学期正式选修过他讲授的微分几何课程。当时我是物理系的三年级学生。

　　张：这门课您有所得益吧?

　　杨：当然。不过我已经记不清楚上课的情形了，只有一件事印象很深：如何证明每一个二维曲面保角等价于平面?我知道如何把度量张量化成

　　的形式，但是想了很久都想不出怎样使A=B。有一天，陈先生告诉我要用复变量，并写下：

　　这个式子。学到这简单的妙诀，是我毕生难忘的经历。

　　张：您何时到达美国?

　　杨：1945年11月。到美国后，我想追随费米或维格纳学物理。但我在哥伦比亚大学找不到费米，因为他在1942年前已离去。于是我去普林斯顿大学找维格纳，却发现他下一年度休假，令我大为失望。幸好我听说费米将回到芝加哥一个新成立的研究所去，这就是我去芝加哥大学读博士学位的缘由。

　　张：陈省身先生有一段很长的时间在芝加哥大学当教授。

　　杨：是的，但这是我1949年离开芝加哥后的事。陈先生在1949年初到美国后，我们经常在普林斯顿、芝加哥和伯克利见面。

　　张：那时你们讨论过纤维丛吗?

　　杨：70年代之前从未谈起过。我们早期的接触是非学术性的。我们谈论过很多数学家，却未讨论过数学。

　　1954年杨振宁和米尔斯的论文

　　在昆明和芝加哥做研究生时，杨振宁已经对规范不变性决定一切电磁相互作用的事实有深刻的印象。这课题能为人所知晓，是自外尔、福克、伦敦在1918—1929年间所做的工作，以及后来泡利的综述文章开始的。但到了40年代和50年代初，这一课题在物理学中仍然只占有一个微不足道的纯技术性的位置。在芝加哥，杨振宁试图把规范不变性推广到非交换群的情形 (电磁场的规范群是交换群U(1)) 。类似于麦克斯韦方程，他尝试把场强

　　定义为：

　　(1)

　　这似乎是麦克斯韦电磁场方程的自然推广，但是“结果出现麻烦，不得不放弃”[1，p. 19]。

　　1954年杨振宁到纽约长岛的布鲁克海文国家实验室访问研究时，再次回到推广规范不变性的想法上来。来自哥伦比亚大学获得博士学位的米尔斯来到该实验室做博士后，和杨振宁在同一办公室工作。杨振宁将非交换规范场的想法介绍给米尔斯，他们决定在(1)式的右边添加一个二次项

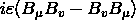
　　结果把一切“麻烦”都消除了，并引出一种很漂亮的新场论。1954年夏，他们向《物理评论》提交了一篇论文，此论文在当年10月发表，标题是“同位旋守恒和规范不变性”[2]。关于这段时期，米尔斯后来写道[4，p. 463]：

　　我当时接受了一个博士后的工作，也在布鲁克海文，并与杨振宁在同一个办公室工作。(当时我正在纽约的哥伦比亚大学的克罗尔指导下慢慢地撰写对于四阶兰姆位移可能有的贡献进行研究的毕业论文。)杨振宁当时已在许多场合中表现出了他对刚开始物理学家生涯的青年人的慷慨，他告诉我关于推广规范不变性的思想，而且我们较为详细地做了讨论。我当时已有了有关量子电动力学的一些基础，所以在讨论中能有所贡献(特别是关于量子化的过程)，而且在计算它的表述形式方面也有小小的贡献，但是一些关键性的思想都是属于杨振宁的。

　　张：我看过有报道说，米尔斯当时在英国[4. p. 463]：“1954年，杨振宁在美国，米尔斯在英国，他们构造了一种涉及非交换群的麦克斯韦方程的非线性推广。”

　　杨：那是不正确的。1954年米尔斯确实是在美国。后来他曾多次访问英国，但绝不是1954年。

　　张：梅耶 (M. E. Mayer) 在1977年出版的一本书里，曾这样写道：

　　读了Yang和Mills的论文，就可以看出他们一定明白了规范势的几何意义，因为他们使用了规范协变的微分与联络的曲率形式。此外，该文的基本方程将与从更为几何的考虑而导出的方程相符······[5，p. 2]

　　梅耶认为你们已经清晰地理解了微分几何，是这样的吗?

　　杨：不，不是这样的。米尔斯和我在1954年所做的事，只是想推广麦克斯韦方程。我们并不清楚麦克斯韦方程的几何意义，也没有朝那个方向去想。对物理学来说，规范势根植于我们对电磁场的描述，而联络是一种几何概念，我是在1970年前后才了解的。麦克斯韦方程原来具有很深的几何意义，是物理学家意想不到的新发现。

　　张：一个有趣的问题是，你在1954年是否理解这篇关于非交换规范场论的原创论文的巨大重要性?

　　杨：喔，恐怕不会。在20世纪50年代，我们只觉得这篇文章很重要；到了60年代，才觉察到它的重要性；及至70年代，才晓得它对物理学是极为重要的。只是到了1974年以后，我才清楚认识到它跟数学的关系。

　　张：众所周知，外尔是规范理论的创始人，为什么你们在1954年的论文中没有提到他?

　　杨：在20世纪40至50年代，物理学家虽然知道外尔曾经导出交换的规范不变概念，但大多只引用泡利的评论文章[6，7]。事实上，我那时并没有看过外尔的任何论文。

　　张：你在普林斯顿见过外尔吗?

　　杨：当然见过，1985年，我在苏黎世纪念外尔百年诞辰的演讲中曾提到这件事：

　　当我在1949年成为普林斯顿高等研究所的一名年轻成员时，曾见过外尔。之后的几年 (1949-1955) 内，我时常看到他。他很容易亲近，但我不记得曾和他讨论过物理学或数学问题。在物理学家中，没有人知道他对规范场思想的兴趣是锲而不舍的。无论是奥本海默还是泡利，都从未提及这一点。我猜测他们也没有把我和米尔斯1954年发表的论文告诉他。如果他们告诉了他，或者他偶然发现了我们的文章，那么我能想象得到，他一定会非常高兴，而且会非常激动。因为我把他所最珍爱的两样东西——规范场和李群——放在一起了。[8，pp. 19–20]。

　　张：我从你的这篇有关外尔的漂亮文章中，知道外尔创立了中微子的二分量理论。

　　杨：是的。外尔在1929年所写的论文中提出了这一理论，但指出它违背了左右对称性，因此不能与现实有关。大约三十年以后，在1956-1957年间，当发现左右对称性并不严格地被遵守的时候，外尔的理论复活了。时至今日，这仍然是有关中微子的正确理论。顺便说一句，在外尔去世两年以后，我和太太买了外尔在普林斯顿的房子，并在那里住了九年之久：1957—1966。

　　张：当外尔知道他的中微子理论获得证实时，有怎样的反应?

　　杨：在1957年物理学界发生巨大轰动的两年之前，外尔不幸去世了。1957年初，发现左右对称不被严格遵守 (即宇称不守恒) 后，外尔的理论复活了。它与μ-衰变的实验极漂亮地吻合。但此后的六个月，物理学界又陷入关于β-衰变的困惑，这一问题与外尔的中微子究竟是右旋还是左旋有关。到这年的秋天，出现了关于β-衰变结构的V-A建议。到了12月，一个精巧的实验将一切问题都澄清了，其中包括外尔中微子是左旋的结论。

　　张：外尔比杨振宁年长37岁，他们属于不同的学术时代，来自不同的国家，从事不同的学科。我们是否可以说外尔是非常欣赏物理的数学家，而杨振宁则是非常欣赏数学的物理学家?

　　Yang-Mills理论与几何学

　　在杨振宁和米尔斯的原始论文发表以后，涉及规范理论的量子化和重整化、寻求Yang - Mills方程的精确解的论文大量涌现，但只有少数人注意到规范场论的几何与拓扑意义，其中包括S. Mandel - stam(1962)，E. Lubkin(1963)和H. G. Loos(1967)。此外，R. Hermann为物理学家写了一系列数学读物，其中一部分也涉及规范场和几何的关系，不过这些工作似乎都没有产生很大的影响。于是我向杨振宁先生询问他了解规范场论与几何学之间的关系的个人体验。

　　张：1954年以后，您曾继续研究规范理论吗?

　　杨：是的，我一直在研究。在20世纪50年代和60年代，虽然物理学中还没有实际地使用非交换规范场论，但是随着时间的推移，越来越多的人欣赏到它的优美特性。例如在1964年，D. Ivanienko出版了一册辑录了12篇译成俄文的关于规范场论的论文集，这些论文的作者包括Yang - Mills，Lee - Yang，J. J. Sakurai，M. Gell - Mann等。我自己在整个20世纪50年代都在规范场论的各个方面做工作，虽然没有获得多少有用的结果。

　　到了20世纪60年代末期，我开始用不可积相因子的方法重新建立规范场论。有一个学期，我正在讲授广义相对论，突然注意到规范场论中的公式

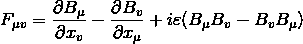
　　（2）

　　与黎曼几何中的曲率公式

　　（3）

　　不仅十分相似，而且如果把二者的符号正确地等同起来，这两个公式乃是完全一样的。当我理解到这一点时，我内心的震撼是难以形容的。

　　张：这是你第一次觉察到规范场论与微分几何之间有密切联系吗?

　　杨：我早先曾注意到Levi - Civita的平行移动和规范场论中的不可积相因子之间的相似性，但我真正领略到二者之间的精确联系，是在我认识到公式(1)与(2)完全一样的那一瞬间。

　　怀着想弄清楚规范理论的几何意义的想法，我向一位杰出的几何学家赛蒙斯(J. Simons)请教，他当时是纽约州立大学石溪分校的数学系主任。赛蒙斯告诉我，规范理论一定与纤维丛上的联络有关。这之后，我试图从阅读斯廷罗德(N. E. Steenrod)的《纤维丛的拓扑学》这类书去了解纤维丛理论，结果却一无所获。对物理学家而言，现代数学的语言实在太乏味、太抽象了。

　　张：我想，只有数学家才会欣赏今天的数学语言。

　　杨：我告诉你一个有关的故事。大约在十年前，我在韩国汉城做演讲，开个即兴玩笑说：“现今只有两类现代数学著作：一类是你看完第一页就不想看下去了，另一类是你看完第一句话就不想看下去了。”后来《数学情报员》杂志还把我这个玩笑刊登出来。但是我猜想，很多数学家都会同意我的看法。

　　张：你在什么时候弄懂了纤维丛理论?

　　杨：1975年初，我邀请赛蒙斯教授给我们做一系列有关微分形式和纤维丛理论的午餐演讲，他欣然接受了这一邀请。于是我们学到了deRham定理、微分形式、拼接 (patching) 等。这些演讲非常有用，使我们理解了物理学中Aharonov - Bohm实验和狄拉克磁单极的量子化条件的数学含义。曹宏生和我后来还弄懂了美妙的Chern - Weil定理。回顾起来，正是这些演讲，使我理解了过去理解得不甚清楚的流形的概念。

　　Yang-Singer-Atiyah

　　张：赛蒙斯的演讲促使杨振宁和吴大峻写了一篇著名的论文：《不可积相因子的概念与规范场的整体表述》[9]。在这篇论文里，他们分析了电磁场的内蕴含义，特别强调了它的整体拓扑性质。他们讨论了Aharonov-Bohm实验和狄拉克磁单极的量子化条件的数学意义。他们还展示了如下的一个字典 (后来被称为“吴–杨字典”) ：

　　?是广义下的电荷和电流。

　　半年后，即1976年夏天，麻省理工学院的数学家辛格 (I. M. Singer) 教授来纽约州立大学石溪分校访问，并和杨教授做了详细的讨论。Singer在大学里原本是学物理的，20世纪40年代转入数学系做研究生。他在1985年这样写道：

　　三十年后，我发现自己在牛津大学讲规范场理论，从吴大峻和杨振宁的字典讲起，最终得到了瞬子，即杨–米尔斯方程的自对偶解。做了三十年的数学，我似乎又回到了物理学[10，p. 200]。

　　为了阐述过去十年的发展，Singer在这篇文章里引用了吴–杨的字典。

　　1977年四五月间，一份由Atiyah，Hitchin，Singer[11]合著的预印本被广泛传阅。在这篇文章里，Atiyah-Singer的指标定理被应用到自对偶规范场上去，由此而引发了许多数学家对规范场的兴趣。

　　1979年，Atiyah出版了一个专题研究报告，题目是“杨–米尔斯场论的几何学”[12]。他的《论文选集》第五卷以“规范场理论”为标题。在杨振宁石溪的办公室的书架上，我发现了一册有Atiyah签名的第五卷《论文选集》。在前言中，Atiyah写道[13]：

　　从1977年开始，我的兴趣转向规范场理论，以及几何学和物理学的互动。一直以来，我对理论物理的兴趣不大，大多数的冲击都来自跟麦凯(George Mackey)的深入讨论。1977年的动因来自两个源泉。一方面，Singer告诉我Yang-Mills方程，通过杨振宁的影响，它正在向数学圈渗透。当Singer在1977年初访问牛津时，他与Hitchin和我周密地考察了自对偶方程。我们发现，简单应用指标定理，就可以得出关于“瞬子”的参数个数的公式。另一个动因则来自彭罗斯(Roger Penrose)和他的小组。

　　张：在吴–杨字典中，你们为什么留下一个问号?

　　杨：因为那时数学家不曾探究过物理学家十分熟悉的重要概念：源，通常用J表示。在麦克斯韦对库仑定律和安培–麦克斯韦定律的联合表述中，这是一个关键的概念。用现代数学来写，就是：

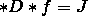
　　其中?是Hodge对偶。在“无源”(J=0)的情形，则可以写成

　　当

　　(依据±号的选取，f分别称为自对偶与反自对偶的) 时，此方程自动满足 (因为f本身还满足另一组麦克斯韦方程

　　，这是法拉第定律和高斯定律的联合表述) 。正是这个原因，许多数学家和物理学家开始研究自对偶与反自对偶的Yang-Mills方程。

　　张：这是一个极有趣的故事。自对偶规范场的研究后来引出了许多优美的数学，包括菲尔兹奖得主唐纳森的工作 (下面还会提到) 。

　　杨：是的，这故事正好提供了一个现代的例子，就是数学家可以从物理学衍生某些概念，这其实在几个世纪以前是很普遍的，不幸的是，现在很少见了。

　　张：有些数学概念对物理学也会变得重要，对此你有什么意见?我们会想起爱因斯坦曾被劝告去注意张量分析，这和你从赛蒙斯那里得到了帮助是否类似?

　　杨：爱因斯坦有博大精深和令人惊叹的洞察力，不宜将后人和他相提并论。至于数学渗入广义相对论与规范场理论的过程，是完全不同的。就前者而言，爱因斯坦没有黎曼几何就不可能写出广义相对论的方程；就后者而言，规范场论的方程早已写出来了，但后来是通过数学才了解其深意。

　　张：曾有许多学者早就指出，规范场论和纤维丛理论密切相关，为什么他们的论文不如你们的论文在数学界有影响力?

　　杨：这可能有许多原因。有些工作太形式化，以至于物理学家不能理解它究竟说了些什么;有些是由于物理内容没有被充分揭示，使得数学家觉得太微不足道。至于吴大峻和我在1975年所写的论文，关于Aharonov-Bohm实验和狄拉克磁单极的量子化条件的讨论，都有助于引起人们的关注。当然，那个字典也很有用。

　　张：你和Singer、Atiyah有过学术交往吗?

　　杨：我多次见过他们，但没有学术合作。

　　Yang-Baxter方程

　　杨振宁为数学界提供的另一重要数学结构，是Yang-Baxter方程，这是从他在统计力学的工作中引出的。

　　1967年，杨振宁试图找出在δ-函数相互作用下，一维费米子多体问题的本征函数[14]。这是一个相当困难的问题。他在求解过程中，揭示出关键的一步是以下的矩阵方程：

　　(4)

　　数年之后，Baxter在解另一个物理问题 (八顶点模型) 时，再次得到矩阵方程(4)。之后有好几个研究中心都朝着这两个发展方向进行研究，尤其是苏联，更集中了人力去研究。1980年，L. D. Faddeev采用了“Yang-Baxter关系”或“Yang-Baxter方程”的术语。时至今日，这一命名已被广泛接受。(1985年，Vladimir Drinfeld还定义了所谓的Yangian以纪念杨振宁，这与量子Yang-Baxter方程有关。)

　　最近六七年以来，数学和物理学上许多激动人心的进展表明，Yang-Baxter方程是与许多数学分支有关的一个基本数学结构，这些分支包括：纽结和辫群理论、算子理论、Hopf代数、量子群、三维拓扑、微分方程的单值化等。就这些课题而发表的工作造成了文献爆炸[10-12]。

　　张：Yang-Baxter方程不过是一个简单的矩阵方程，为何会有那么大的重要性呢?

　　杨：在最简单的情况下，该方程可以写为

　　(5)

　　这是关于辫群的Artin基本方程。显然，编辫子是一系列置换的历史记录。我们也不难理解，许多数学和物理问题与一连串置换的历程有密切关系。

　　从最近六七年的进展来看，我感觉，Yang-Baxter方程是继Jacobi恒等式

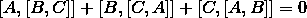
　　(其中[A,B]=AB?BA是换位子)之后最基本的代数方程。大家都知道，Jacobi恒等式是整个李代数理论及相关的李群理论的起点。

　　张：Yang-Baxter方程对数学的影响似乎比对物理的影响更大?

　　杨：目前是如此。实际上，有些物理学家认为，Yang-Baxter方程是纯数学，我认为这看法将会改变。Yang-Baxter方程是一个基本结构，不论物理学家是否喜欢，最终必然要使用它。在20年代，许多物理学家称群论为“害”(group pest)。这种观念一直持续到30年代，但此后就消失了。

　　1986年和1990年的菲尔兹奖

　　Yang-Mills理论和Yang-Baxter方程，两者都在当今核心数学中占重要位置，从1986年和1990年的菲尔兹奖的颁发就可以看出这一点。

　　唐纳森在1986年于伯克利举行的国际数学家大会上获得菲尔兹奖。Atiyah这样介绍唐纳森的工作[19]：

　　如果跟弗里德曼 (Freedman) 的一项重要工作合在一起，唐纳森的结论意味着：存在一个“怪异”的四维空间，它与标准的欧几里得空间同胚，但不微分同胚······他们的结果来自理论物理中的Yang-Mills方程，它是麦克斯韦方程的非线性推广。

　　1990年的国际数学家大会有四位菲尔兹奖得主：德林费尔德 (Vladimir Drinfeld)、琼斯 (V. F. R. Jones)、森重文 (Shigefumi Mori) 和威腾 (E. Witten) 。除森重文外，其他三人的工作都跟Yang-Mills方程或Yang-Baxter方程有关。以下的引文摘自1990年在京都举行的国际数学家大会上的报告：

　　我们要提到德林费尔德和马宁(Manin)在构造瞬子方面的先驱性工作。这些是自对偶Yang-Mills方程的解······德林费尔德在物理学上的兴趣，继续保持在Yang-Baxter方程的研究上[20，p. 1210]。

　　琼斯认识到，在某些条件下，Yang-Baxter方程可用来构造链环(link)的一些不变量，从而开启了一个新的方向······量子群理论和非交换Hopf代数被神保道夫 (Michio Jimbo) 和德林费尔德用来构造Yang-Baxter方程的解[21，p. 1210]。

　　威腾用这些观念描述了唐纳森和弗洛尔(Floer)的不变量 (Atiyah早先想法的推广)，并且将琼斯的纽结多项式推广到任意的环绕三维流形(ambient 3-manifold)上[22，p. 1214]。

　　我也颇有兴趣地注意到，在京都国际数学家大会上的大会报告过分倾向于数学物理，人们有过一些抱怨[23]：

　　到处听到的都是量子群、量子群、量子群!

　　数学和物理

　　张：为什么您在物理上的工作会对数学产生这么大的影响?

　　杨：这是一个很难回答的问题。幸运是一个因素。除此之外，以下两点可能有关。首先，如果你选择去做原始的问题，那么你就有较大的机会接触到数学的基本结构。其次，你必须对数学的价值观有某种程度的欣赏。

　　张：请就第一点做进一步的说明。

　　杨：理论物理中的好多文章是这样产生的：甲发表了一篇论文阐述他的理论，乙说他的论文改进了甲的结果，后来丙指出乙的理论是错误的，甚至往往最后发现甲的原始概念是完全错的或者根本没有意义。

　　张：数学界同样有类似的情形。

　　杨：不，不，情况极为不同。数学定理都是被证实过的，或被认为是证实过的。在理论物理界，我们就像在做猜谜游戏，而大多数猜测又往往是错的。

　　张：不过，读最新的文献是必要的。

　　杨：那当然对，了解你从事的领域中别人在想些什么，当然是重要的。但是要取得实质性的进展，就必须面对原始的简单物理问题，而不是别人的猜想。

　　张：您和米尔斯在1954年提出规范场正是这样做的吗?

　　杨：是的，我们问自己：“我们能否把麦克斯韦方程加以推广，从而得到粒子相互作用的一般法则呢?”

　　张：那么，Yang-Baxer方程又是怎么一回事呢?您在1967年的论文里讨论的并不是物理学里的一个基本重要的问题。

　　杨：你说得对。但是，我是在探究量子力学里一个最简单的数学问题：具有最简单的相互作用的一维费米子的系统。

　　张：为什么您强调“最简单”?

　　杨：因为问题越简单，你的分析工作就越可能接近某些基本的数学结构。让我用以下的比喻来阐明。假如象棋与围棋中有一者被发现具有一个以数学为基础的获胜策略，那么一定是围棋，因为围棋较为简单和基本。

　　张：请您再谈谈第二点成功秘诀。

　　杨：许多理论物理工作者在某些方面对数学有抗拒的心理或者有贬低数学的倾向。我不赞同这种态度，我曾经这样写道[1，p. 74]：

　　我的物理学界同事大多对数学采取功利主义的态度。也许因为受我父亲的影响，我较为欣赏数学。我欣赏数学家的价值观，我赞美数学的优美和力量：它有战术上的技巧与灵活，又有战略上的雄才远虑。而且，堪称奇迹中的奇迹的是，它的一些美妙概念竟是支配物理世界的基本结构。

　　张：您父亲对你有哪些数学影响?

　　杨：举例来说吧。当我还是中学生的时候，就从父亲那里接触到群论的基本原理，也常常被父亲书架上的一本斯派泽关于有限群的书中的美丽插图所迷住。当我写大学论文时，父亲建议我读一读迪克森所写的一本小书，叫做《近世代数理论》。这本书有短短20页的一章介绍了群表示的特征标理论的要点。这一章的优美和威力，使我认识到群论无与伦比的美妙和力量。

　　张：据说你曾经当过中学数学老师，而且杨夫人(杜致礼)就是你授课班上的学生。

　　杨：是的。我曾在1944-1945年间，在昆明的一所中学里教数学，她是我班上的学生。但那时我们并不熟悉。好几年之后，我在普林斯顿和她邂逅。教数学是一桩有趣的经历，不过这跟我对数学的态度并没有关系。

　　张：你认为物理学家多学一点数学是否重要?

　　杨：不，如果一个物理学家学了太多的数学，他或她将可能被数学的价值观所吸引，并因而丧失自己的物理直觉。我曾经把数学和物理之间的关系比喻为一对树叶，它们只在基部有很小的共同部分，而其余大部分是分开的：

　　它们有各自的目标和截然不同的价值观与传统。在基础概念的层面，它们令人惊讶地共享着某些概念，但即使如此，每个学科仍旧按着自身的脉络生长着。

　　张：对物理学来说，学习实验结果是否更重要?

　　杨：是的。

　　张：你曾和许多数学家有过交往吗?

　　杨：有一些。当李政道和我在1951年研究后来被称为“单位圆定理”的时候，Von Neumann和A. Selberg曾建议我们去读G. Pólya和Szego的著作《分析中的问题和定理》。1965年H. Whitney曾向我和我的弟弟杨振平讲解向量场的指数(index)的拓扑概念。为了求解Wiener-Hopf积分方程，M. Kac曾建议我们读M. G. Krein有关这一课题的长篇综述。到了70年代，我曾和复旦大学以谷超豪为首的数学小组进行合作。除了这里提到的赛蒙斯讲座之外，我还得益于跟普林斯顿高等研究院A. Borel的交往，也得益于纽约州立大学石溪分校数学系的同事：Ronald G. Douglas，M. Gromov，I. Kra，B. Lawson，萨支汉(C. H. Sah)①和其他人。

　　①美国著名数学家，1934年出生于北京，是物理学家萨本栋次子。

　　张：你和陈先生有很多的交往吗?

　　杨：如上所述，我早年在中国曾选修过他讲述的微分几何课，也可能旁听过他的其他课程。在1949年及以后的几年，我们曾多次见面，但未曾深谈数学。在20世纪50年代，我已经说过陈氏级(Chern class)的重要性，但并不知道它的奥妙。

　　只是到了1975年，当赛蒙斯在我们的理论物理研究所做了一系列演讲之后，我才终于明白了纤维丛和纤维丛上的“联络”的基本概念。经过一番努力，我也终于明白了最基本的陈–韦伊 (Chern-Weil) 定理。

　　我在懂得这深奥美妙的定理后，真的有了触电的感觉。这个感受犹胜于60年代了解外尔(Weyl)计算群表示的特征标公式和彼得–外尔(Peter-Weyl)定理之后的喜悦。为什么呢?可能是因为陈–韦伊定理更“几何”一点吧。

　　而且，感受并不止于此。还有更深刻、更触及心灵深处的地方：到头来忽然领悟到，客观的宇宙奥秘与纯粹用逻辑和优美这些概念发展出来的数学概念竟然完全吻合，那真是令人感到悚然。我曾经描述过这个感受[1，p. 567]：

　　在1975年，明白了规范场和纤维丛理论之间的关系之后我非常激动。我开车到陈省身教授在伯克利附近的El Cerrito寓所······我说，物理学上的规范场正好是纤维丛上的联络，而后者是在不涉及物理世界的情况下发展出来的，这实在令我惊讶。我还加了一句：“这既令我惊讶，也令我迷惑不解，因为你们数学家凭空梦想出这些概念。”陈省身当即提出异议：“非也，非也，这些概念并非是凭空梦想出来的，它们既是自然的，也是实在的。”

　　参考文献

　　[1] C. N. Yang, Selected Papers, 1945-1980, with Commentary, W. H. Freedman and Company, San Francisco, 1983.

　　[2] C. N. Yang and R. L. Mills, \Conservation of isotopic spin and isotopic gauge invariance," Phys. Rev. 96 (1954), 191-195.

　　[3] R. Mills, \Gauge ˉelds," Ann. J. Phys. 57 (1989), 493-507.

　　[4] P. A. Gri±th, \Mathematical sciences: A unifying and dy-namical resource{Report of the Panel on Mathematic Sciences, initiated by the National Research Council," Notices AMS 33 (1986), 463.

　　[5] W. Drechsler and M. E. Mayer. Fibre Bundle Techniques in Gauge Theories, Lecture Notes in Physics No. 67, Springer-Verlag, Berlin, 1977, p. 2.

　　[6] W. Pauli, Handbuch der physik, 2nd ed. (Geiger and Scheel, 1933) Vol. 24(1), p. 83.

　　[7] W. Pauli, Reviews of Modern Physics 13, 203 (1941).

　　[8] C. N. Yang, \Herman Weyl's contributions to physics," in Her-man Weyl (1885|1955). Springer-Verlag, Berlin, 1985.

　　[9] T. T. Wu and C. N. Yang, \Concept of nonintegrable phase factors and global formulation of gauge ˉelds," Phys. Rev. D 12 (1975), 3845-3857.

　　[10] I. M. Singer, \Some problems in the quantization of gauge the-ories and string theories," Proc. Symposia in Pure Math. 48 (1988), 198-216.

　　[11] M. F. Atiyah, N. J. Hitchin, and I. M. Singer, \Self-duality in four-dimensional Riemann geometry," Proc. Roy. Soc. London Ser. A, 362 (1978), 425{461.

　　[12] M. F. Atiyah, Geometry of Yang-Mills Fields, Scuola Normale Superiore, Pisa, 1977.

　　[13] M. F. Atiyah, Collected Works, Vol. 5. Gauge Theories. Cam-bridge University, Press, Cambridge, England, 1988, p. 1.

　　[14]    C. N. Yang, \Some exact results for the many-body problem in one dimension with repulsive delta-function interaction," Phys. Rev. Lett. 19 (1967), 1312-1315.

　　[15]    R. J. Baxter, \Partition function of the eight-vertex lattice model," Ann. Phys. 70 (1972), 193-228.

　　[16] M. Barber and E. Pearce, eds., Yang-Baxter Equations, Con-formal Invariance and Integrability in Statistical Mechanics and Field Theory, World Scientiˉc, Singapore, 1990.

　　[17] M. Jimbo, ed., Yang-Baxter Equation in Integrable Systems, World Scientiˉc, Singapore, 1990.

　　[18] C. N. Yang and M. L. Ge, eds., Braid Group, Knot Theory and Statistical Mechanics, World Scientiˉc, Singapore, 1989.

　　[19] M. F. Atiyah, \The work of Donaldson," Notices AMS 33 (1986), 900.

　　[20] A. Ja?e and B. Mazur, \Vladimir Drinfeld," Notices AMS 37 (1990), 1210.

　　[21] R. H. Hermann, \Vaughan E R. Jones," Notices AMS 37 (1990), 1211.

　　[22] K. Galwedzki and C. Soule, \Edward Witten," Notices AMS 37 (1990), 1214.

　　[23] Mathematical Intelligencer, vol. 9 (1991), no. 2, 7.

　　附 

　　杨振宁是当代的大物理学家，又是现代数学发展的重要推动者，他的两项巨大成就——杨–米尔斯规范场和杨–巴克斯特方程，成为80年代以来一系列数学研究的出发点，其影响遍及微分几何、偏微分方程低维拓扑、纽结理论、量子群等重大数学学科。笔者曾在杨振宁与当代数学的访谈录中有过较为详细的介绍，这里记录的有关数学与物理学的关系，来自笔者在1995年末在纽约州立大学访问杨振宁时的一些谈话材料。

　　1.  有关数学的两则笑话

　　20世纪80年代初，杨振宁在韩国汉城做物理学演讲时说，“有那么两种数学书，第一种是你看了第一页就不想看了，第二种是你看了第一句话就不想看了。”当时引得在座的物理学家哄堂大笑。此话事出有因。1969年，杨振宁觉得物理上的规范场理论与数学上的纤维丛理论可能有关系，就把著名拓扑学家Steenrod写的《纤维丛的拓扑学》一书拿来读，结果是一无所获。原因是，该书从头至尾都是定义、定理、推论式的纯粹抽象演绎，生动活泼的实际背景淹没在形式逻辑的海洋中，使人摸不着头脑。

　　杨振宁在汉城演讲中的那句话本来是即兴的玩笑，不能当真的。岂料不久之后被《数学情报员》爆料出来，公之于众。数学界当然会有人反对，认为数学书本来就应该是那样写的。不过，杨振宁先生说，“我相信会有许多数学家支持我，因为数学毕竟要让更多的人来欣赏，才会产生更大的效果。”

　　我想，在当代物理学家中，杨振宁是特别偏爱数学而且大量运用数学的少数人之一。如果连他也对某些数学著作的表达方式啧有烦言，遑论其他的物理学家?就更不要说生物学家、经济学家、一般的社会学家和读者了。

　　杨振宁先生讲的另一个笑话，可在波兰裔美国数学家Ulam的自传《一个数学家的遭遇》中读到，该书第294页写道：

　　杨振宁，诺贝尔物理学奖得主，讲过一个有关当前数学家和物理学家之间不同思考方式的故事：一天晚上，一帮人来到一个小镇。他们有许多衣服要洗，于是满街找洗衣房。忽然他们见到一扇窗户上有标记：这里是洗衣房。一个人高声问道：“我们可以把衣服留在这里让你洗吗?”窗内的老板回答说：“不，我们不洗衣服。”来人又问道：“你们窗户上不是写着是洗衣房吗?”老板又回答说：“我们是做洗衣房标记的，不洗衣服。”这很有点像数学家。数学家只做普遍适合的标记，而物理学家却创造了大量的数学。

　　杨振宁教授的故事是一则深刻的寓言。数学圈外的人们对于数学家“只做标记，不洗衣服”的看法是不赞成的。数学家Ulam在引用了杨振宁的笑话之后，问道，信息论是工程师Shannon创立的，而纯粹数学家为什么不早就建立起来?他感叹地说：“现今的数学与19世纪的数学完全不同，甚至99%的数学家不懂物理，然而有许许多多的物理概念，要求数学的灵感、新的数学公式、新的数学观念。”

　　2.理论物理的“猜”与和数学的“证”

　　1995年12月，杨振宁先生接到复旦大学校长杨福家的来信，邀请杨振宁在1996年5月到复旦大学为“杨武之讲座”做首次演讲。杨武之教授是杨振宁的父亲，又是我国数学前辈，早年任清华大学数学系主任多年，50年代后，则在复旦大学任教授。所以杨振宁很愉快地接受了邀请，但是他不能像杨福家校长要求的那样做20次演讲，只准备讲三次。顺着这一话题，杨振宁先生又谈了理论物理和数学的一些关系。杨先生说：

　　理论物理靠的是“猜”，而数学讲究的是“证”，理论物理的研究工作是提出猜想，设想物质世界是怎样的结构。只要言之成理，不管是否符合现实，都可以发表。一旦猜想被实验证实，这一猜想就变成真理。如果被实验否决，发表的论文便一钱不值(当然失败是成功之母，但那是另一层意思了)。数学就不同，发表数学论文只要没有错误，总是有价值的，因为那不是猜出来的，而是有逻辑的证明。逻辑证明的结果，总有一定的客观真理性。

　　正因为如此，数学的结果可以讲很长时间，它的结果以及得出这些结果的推导过程都是很重要的。高斯给出代数基本定理的四种证明，每种证明都值得讲。如果让丘成桐从头来讲卡拉比猜想的证明，他一定会有20讲。但是，要我讲宇称不守恒是怎么想出来的，我讲不了多少话。因为当时我们的认识就是朝着否定宇称守恒的方向想，“猜测”不守恒是正确的。根据是有一些，但不能肯定。究竟对不对，要靠实验。

　　杨先生最后说：“理论物理的工作好多是做无用功，在一个不正确的假定下猜来猜去，文章一大堆，结果全是错的。不像数学，除了个别错的以外，大部分都是对的，可以成立的。”

　　杨先生的这番话，使我想起不久前Quine和Jaffe的一篇文章①，发表于Bulletin of AMS1993年8月号，曾引起相当的轰动。该文的主题是问，是否允许“猜测数学”存在？文中提到，物理学已经有了分工，理论物理做“猜测”，实验物理做“证明”。但是数学没有这种分工。一个数学家，既要提出猜想，又要完成证明。除了Hilbert那样的大人物可以提出23个问题，其猜想可以成为一篇大文章之外，一般数学家最多在文章末尾提点猜想以增加读者的兴趣，而以纯粹的数学猜想为主干的文章是无处发表的。因此，两位作者建议允许“理论数学”即“猜测数学”的存在。

　　①A. Jaffe and F. Quine, "Theoretical mathematics: toward a cultural synthesis of mathematics and theoretical physics," Bull. Amer., Math. Soc. N. S. 29 (1993), 1-13; M. Atiyah et al., "Responses," Bull. Amer. Math. Soc. N. S. 30, (1994), 178-207. (中译文分别是: "理论性数学: 数学与理论物理的文化综合", 周善有译,《数学译林》1993 年第 13 卷第 2 期, 147{157; 对 A. Jaffe 与 F. Quine 的《理论性数学: 数学与理论物理的文化综合》一文的反应, 江嘉禾、铁小匀译,《数学译林》1994 年第 13 卷第 4 期, 317-322.)

　　这样一来，现在有两种互相对立的看法。一方面，物理学界中像杨振宁先生那样，觉得理论物理的研究太自由，胡乱猜测皆成文章，而数学的情况还是比较好的。另一方面，数学界如Quine和Jaffe那样，觉得目前数学研究要求每个结论都必须证明的要求，太束缚人的思想，应该允许人们大胆地猜测，允许有根据但未经完全确认的数学结论发表出来。二者孰是孰非，看来需要一个平衡。许多问题涉及哲学和社会学层面，就不是三言两语可以解决的了。

　　3. 复数、四元数的物理意义

　　虚数的出现可溯源至15世纪时求解三次方程，但直到18世纪的Euler时代，仍称之为“想象的数”(imaginary numbers)。数学界正式接受它，要到19世纪，经Cauchy，Gauss，Riemann，Weierstrass的努力，以漂亮的复变函数论赢得历史地位。至于在物理学领域，一直认为能够测量的物理量只是实数，复数是没有现实意义的。尽管在19世纪，电工学中大量使用复数，有复数的电动势、复值的电流，但那只是为了计算的方便。不用复数，你能算出来，只不过麻烦一些而已。计算的最后结果也总是实数，并没有承认在现实中真有“复数”形态的电流。

　　有鉴于此，杨振宁先生说，直到20世纪初，情况仍然没有多少改变。一个例证是创立了量子波动力学的薛定谔，据说他在1926年初就已经得到我们现在熟悉的方程，

　　（6）

　　其中含有虚数单位i，波函数是复函数，但最后总是取实部。薛定谔因为其中含有虚数，而对方程(1)不满意，力图找出不含复数的基本方程。于是，他将上式两边求导后化简，得到了一个不含复数但更复杂的高阶微分方程：

　　（7）

　　1926年6月6日，薛定谔在给洛伦茨的一封长信中，认为这个不含复数的方程(7)“可能是一个普遍的波动方程”。这时薛定谔正在为消除复数而努力。但是到了同年的6月23日，薛定谔领悟到，这是行不通的。在论文中，他第一次提出：“波函数是时空的复函数，并满足方程(6)。”他把方程(6)称为真正的波动方程，原因是，描述量子行为的波函数，不仅有振幅大小，还有相位，二者相互联系构成整体，所以量子力学方程非用复数不可。另一个例子是Weyl在1918年发展的规范理论，被爱因斯坦拒绝接受，也是因为没有考虑相位因子，只在实数范围内处理问题。后来由Fock和London用加入虚数i的量子力学加以修改，Weyl的理论才又复活。

　　牛顿力学中的量全都是实数量，但一旦进入量子力学，就必须使用复数量。杨振宁和Mills在1954年提出非交换规范场，正是注意到了这一点，才会把Weyl规范理论中的相位因子推广到李群的李代数，从而完成了一项历史性的革命。

　　1959年，Aharanov和Bohm设计一个实验表明，在量子力学中，与标量势一样，向量势也是可以测量的，打破了“可测的物理量必须是实数”的框架。这一实验相当困难，最后由日本的Tonomura及其同事于1982年和1986年先后完成。这样，物理学中的可测量终于拓展到了复数。

　　令我惊异的是，杨振宁教授预言，下一个目标将是四元数进入物理学。自从1843年爱尔兰物理学家和数学家哈密顿发现四元数之后，他本人曾花了后半辈子，试图把四元数像复数那样广泛地运用于数学和物理学，开创四元数的世纪。但结果是令人失望的。人们曾评论这是“爱尔兰人的悲剧”。时至今日，一个数学系的毕业生可能根本不知道有四元数这回事，最多也不过是非交换代数的一个例子而已。我还记得，1986年春，钱学森在致中国数学会理事长王元的一封信中，曾建议多学计算机知识，而把研究“四元数分析”(复分析的推广)的工作贬低为“像上一个世纪的古董”。总之，和许多数学工作者一样，我认为四元数的发现，只不过是“抽象的代数产物”，不会有什么大用处。

　　然而，杨振宁向我解释了他的想法：

　　物理学离不开对称。除了几何对称之外，还有代数对称。试看四元数

　　，其基本单位满足

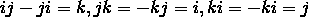
　　像这种对称的性质，在物理学中经常可以碰到。问题是：有哪些基本的物理学规律非用四元数表示不可?现在似乎还没有出现。最近，丘成桐等人的文章说，我在1977年发表的一篇文章，曾推动代数几何中稳定丛的解析处理的理论。我还没有问过数学家，不知道这是怎么一回事。许多工作，包括用四元数表示的物理理论，也许会在这种交流中逐步浮现。

　　杨振宁先生又说，至于将复分析理论形式地推广到四元数分析理论，由于四元数乘法的非交换性，导数无法唯一确定，所以不会有什么好结果出来。现在也有物理学家写成著作，但没有引起什么注意。将来要用四元数表达的物理定律，一定会是一组非线性微分方程组，其解的对称性必须用四元数来表示。所以杨先生相信：“爱尔兰人的悲剧是会变成喜剧的。”

　　4.  “双叶”比喻

　　数学和物理的关系，应该是十分密切的。在数学系以外的课程中，物理系开设的数学课最多最深。“物理学公理化、数学化”(即希尔伯特23个问题中的第6个问题)，曾是一个时期许多大学问家追逐的目标。不过，善用数学与物理的杨振宁教授却认为，二者之间的差别很大，他有一个生动的“双叶”比喻，来说明数学和物理之间的关系。杨振宁认为，数学和物理学像一对“对生的”树叶，它们只在基部有很小的共有部分，大部分则是互相分离的。杨振宁先生解释说：“它们有各自的目标和截然不同的价值观与传统。在基础概念的层面，它们令人惊讶地共享着某些概念，但即使如此，每个学科仍按着自身的脉络生长着。”

　　本文收录于《杨振宁的科学世界：数学与物理的交融》（高等教育出版社，2018）。本文中文版原载：数学传播，1992(4)；科学，1992(4)。英文版刊于Mathematical Intelligencer，1993，15(4)。中文版与英文版内容不全相同，本文由张奠宙译自英文版。本文还有一篇姊妹篇，见于张奠宙主编的《20世纪数学经纬》一书中的同名文章。